SVO: Fast Semi-Direct Monocular Visual Odometry论文阅读笔记
Abstract
- 作者提出了一种半直接单目视觉里程计算法,该算法精确、鲁棒,并且比当前最先进的方法更快
- 该算法无需代价昂贵的特征提取和鲁棒匹配技术
- 该算法直接对像素强度进行操作,在高帧率下可以达到亚像素精度
- 使用显式建模异常测量的概率建图方法来估计3D点,从而得到更少的异常点和更可靠的点
- 精确的高帧率运动估计在纹理较少、重复和高频的场景中具有更高的鲁棒性
- 该算法应用于GPS拒止环境下的微型飞行器状态估计,在机载嵌入式计算机上以55帧/秒的速度运行,在消费级笔记本电脑上以超过300帧/秒的速度运行
- 该算法称为SVO (Semi-direct Visual Odometry),并将软件实现开源
1 Introduction
1.1 Taxonomy of Visual Motion Estimation Methods
- feature-based methods
- 依赖于检测和匹配阈值
- 需要鲁棒估计技术来处理错误的对应关系
- 大多数特征检测器只优化速度而没有优化精度,运动估计中的漂移必须通过平均多个特征测量来补偿
- direct methods
1.2 Related Work
1.3 Contributions and Outline
- SVO使用了特征对应关系,但这是直接运动估计的隐式结果,特征提取只在选择关键帧来初始化新的3D点时需要
- 使用显式建模异常点测量的贝叶斯滤波器来估计特征点的深度
- 本文的贡献如下:
- 一种新颖的半直接VO流程,该方法比现有的最先进的用于MAVs的方法更快更准确
- 集成了一种对异常测量具有鲁棒性的概率建图方法
2 System Overview
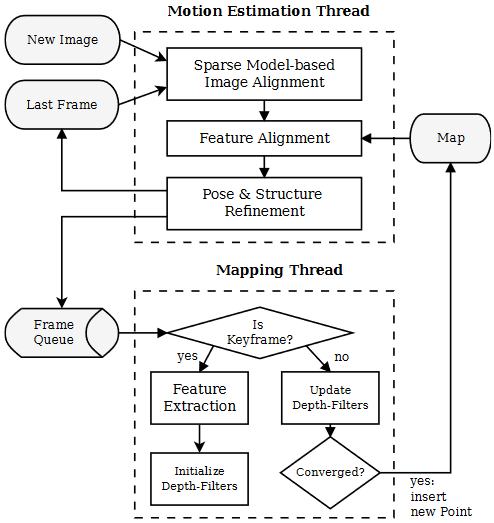
分为运动估计和建图两个并行线程
运动估计线程:
通过基于稀疏模型的图像对齐进行位姿初始化
- 通过最小化同一3D点投影位置对应像素之间的光度误差,找到相对于上一帧的相机位姿
重投影点对应的2D坐标通过相应的特征块对齐进行细化
最小化重投影误差来细化位姿和结构
建图线程:
- 对于每一个待估计3D点的2D特征,初始化一个概率深度滤波器
- 当选择一个新的关键帧时会初始化一个新的深度滤波器
- 以Bayesian的形式更新深度估计
- 当深度滤波器的不确定性足够小时,在地图中插入一个新的3D点
3 Notation
4 Motion Estimation
4.1 Sparse Model-based Image Alignment
连续两帧相机位姿之间的变换矩阵\(\mathbf{T}_{k,k-1}\)的最大似然估计将最小化强度残差的负对数似然: \[ \mathbf{T}_{k, k-1}=\arg \min _{\mathbf{T}} \iint_{\overline{\mathcal{R}}} \rho[\delta I(\mathbf{T}, \mathbf{u})] d \mathbf{u} \tag{1} \]
强度残差\(\delta I\)由观测到同一个3D点的像素之间的光度误差定义: \[ \delta I(\mathbf{T}, \mathbf{u})=I_k\left(\underbrace{\pi\left(\underbrace{\mathbf{T} \cdot \underbrace{\pi^{-1}\left(\mathbf{u}, d_{\mathbf{u}}\right)}_{(a)}}_{(b)}\right)}_{c}\right)-I_{k-1}(\mathbf{u}) \quad \forall \mathbf{u} \in \overline{\mathcal{R}} \tag{2} \]
- 其中\(\overline{\mathcal{R}}\)是第\(k-1\)帧深度\(d_{\mathbf{u}}\)已知的图像域中的反投影点在第\(k\)帧可见的子图像域
- (a)表示根据第\(k-1\)帧图像像素坐标及深度逆投影到三维空间
- (b)表示将三维坐标点变换到第\(k\)帧相机坐标系下
- (c)表示将三维坐标点投影到第\(k\)帧图像平面
假设强度残差服从单位方差的正态分布,最小化负对数似然问题可以转换为最小二乘问题(由于特征点的稀疏性,实际上是最小化特征点周围像素块\(\mathbf{I}(\mathbf{u}_i)\)的强度残差): \[ \mathbf{T}_{k, k-1}=\arg \min _{\mathbf{T}_{k, k-1}} \frac{1}{2} \sum_{i \in \overline{\mathcal{R}}}\left\|\delta \mathbf{I}\left(\mathbf{T}_{k, k-1}, \mathbf{u}_i\right)\right\|^2 \tag{3} \]
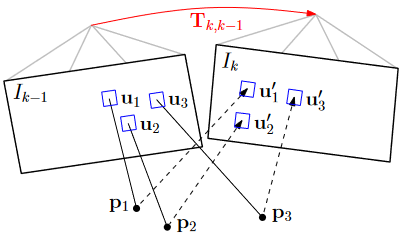
通过Gauss-Newton法求解该非线性优化问题
给定变换矩阵的一个估计\(\hat{\mathbf{T}}_{k, k-1}\),该估计值的增量更新\(\mathbf{T}(\xi)\)可以用\(\xi \in \mathfrak{s e}(3)\)参数化
强度残差使用逆构造公式(inverse compositional formulation)[27]重新表述为: \[ \delta \mathbf{I}\left(\xi, \mathbf{u}_i\right)=\mathbf{I}_k\left(\pi\left(\hat{\mathbf{T}}_{k, k-1} \cdot \mathbf{p}_i\right)\right)-\mathbf{I}_{k-1}\left(\pi\left(\mathbf{T}(\xi) \cdot \mathbf{p}_i\right)\right) \tag{4} \]
- 其中\(\mathbf{p}_i=\pi^{-1}\left(\mathbf{u}_i, d_{\mathbf{u}_i}\right)\)
- 文献[27]中逆构造公式的推导
通过正规方程计算最优更新步长\(\mathbf{T}(\xi)\): \[ \mathbf{J}_i^T\mathbf{J}_i \xi = -\mathbf{J}^T_i \delta \mathbf{I}(0,\mathbf{u}_i) \tag{5} \]
- 其中 \[ \begin{aligned} \mathbf{J}_i &= \nabla \delta \mathbf{I}\left(0, \mathbf{u}_i\right)=\left. \frac{\partial \delta \mathbf{I}\left(\xi, \mathbf{u}_i\right)}{\partial \xi}\right|_{\xi=0} \\&=\left.\left.\left.\frac{\partial \mathbf{I}_{k-1}(\mathbf{a})}{\partial \mathbf{a}}\right|_{\mathbf{a}=\mathbf{u}_i} \cdot \frac{\partial \pi(\mathbf{b})}{\partial \mathbf{b}}\right|_{\mathbf{b}=\mathbf{p}_i} \cdot \frac{\partial \mathbf{T}(\xi)}{\partial \xi}\right|_{\xi=0} \cdot \mathbf{p}_i \end{aligned} \]
更新当前状态\(\hat{\mathbf{T}}_{k, k-1} \longleftarrow \hat{\mathbf{T}}_{k, k-1} \cdot \mathbf{T}(\xi)^{-1}\)
4.2 Relaxation Through Feature Alignment
通过帧间匹配估计相机位姿的方式会产生累积漂移,需要通过相机位姿与地图对齐来进一步约束相机位姿
将地图点反投影到第\(k\)帧图像得到对应的2D特征点坐标\(\mathbf{u}_i^{\prime}\),然后通过最小化第\(k\)帧图像中的特征像素块相对于关键帧\(r\)中的参考特征像素块的光度误差来优化它: \[ \mathbf{u}_i^{\prime}=\arg \min _{\mathbf{u}_i^{\prime}} \frac{1}{2}\left\|\mathbf{I}_k\left(\mathbf{u}_i^{\prime}\right)-\mathbf{A}_i \cdot \mathbf{I}_r\left(\mathbf{u}_i\right)\right\|^2, \quad \forall i \tag{6} \]
- 对参考特征像素块使用仿射变换\(\mathbf{A}_i\)是因为关键帧中使用了更大的特征像素块尺寸,并且最近的关键帧通常比上一帧图像离当前帧更远
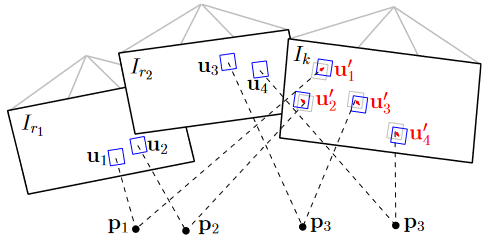
该阶段可以理解为违背对极约束的松弛过程,使特征像素块之间具有更高的相关性(亚像素级精度)
4.3 Pose and Structure Refinement
执行motion-only BA,通过最小化重投影残差来优化相机位姿\(\mathbf{T}_{k, w}\): \[ \mathbf{T}_{k, w}=\arg \min _{\mathbf{T}_{k, w}} \frac{1}{2} \sum_i\left\|\mathbf{u}_i-\pi\left(\mathbf{T}_{k, w} w \mathbf{p}_i\right)\right\|^2 \tag{7} \]
注意:此处误差是像素坐标差异而不是光度误差
执行structure-only BA,通过最小化重投影残差来优化3D点位姿
执行local BA,联合优化关键帧相机位姿和3D点位置
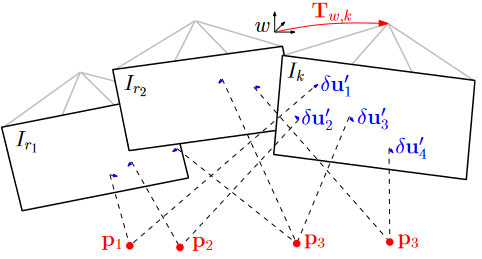
4.4 Discussion
- 讨论了上述三个阶段不可割裂的关系
- 稀疏图像对齐阶段隐式地满足了对极约束,并进行了异常点检测
- 后两个阶段显著地减少了漂移
5 Mapping
给定一张图像及其位姿\(\left\{I_k, \mathbf{T}_{k, w}\right\}\),建图线程估计对应的3D点未知的2D特征点的深度
- 特征点的深度估计采用概率分布建模
- 基于[28]后续观测被用于在贝叶斯框架下更新分布
- 当分布的方差足够小时,2D特征点对应的3D点被插入到地图中,并立即用于运动估计
每个深度滤波器与一个参考关键帧\(r\)中的参考像素块\(\mathbf{u}_i\)(特征角点)相关联,深度均值初始化为参考帧的平均景深,但具有较高的深度不确定性
对于每个后续观测\(\left\{I_k, \mathbf{T}_{k, w}\right\}\),在新图像\(I_k\)的极线上搜索一个与参考像素块\(\mathbf{u}_i\)相关性最高的像素块\(\mathbf{u}_i^{\prime}\),并通过三角化获得对应的深度\(\tilde{d}_i^k\)
测量\(\tilde{d}_i^k\)使用高斯+均匀混合模型分布[28]建模
正常测量值在真实深度\(d_i\)附近服从正态分布,异常测量值在区间\([d_i^{min}, d_i^{max}]\)内服从均匀分布 \[ p\left(\tilde{d}_i^k \mid d_i, \rho_i\right)=\rho_i \mathcal{N}\left(\tilde{d}_i^k \mid d_i, \tau_i^2\right)+\left(1-\rho_i\right) \mathcal{U}\left(\tilde{d}_i^k \mid d_i^{\min }, d_i^{\max }\right) \tag{8} \]
- 其中$_i $是内点概率
该模型的递归Bayesian更新步骤在文献[28]中详细介绍
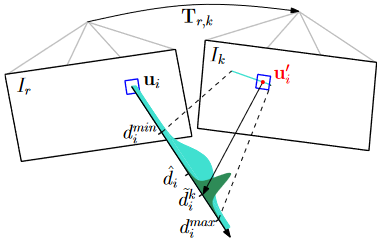
作者使用逆深度坐标来处理大场景深度
6 Implementation Details
- SVO的初始化过程
- 假设前两个关键帧所拍到的特征点在同一个平面上(下视相机),然后估计单应性矩阵,并通过三角化来估计初始特征点的深度值
- 为了应对快速运动的情形,SVO使用由粗到精(coarse-to-fine)的方案执行稀疏图像对齐
- 对图像进行半采样从而创建五层图像金字塔
- 先在最粗糙的层上优化强度残差直至收敛,随后在更精细的层上优化
- 在第三层金字塔收敛后终止该过程
- SVO在地图中保存固定数量的关键帧用于特征对齐和结构细化
- 关键帧选择的标准:新帧相对于最近关键帧的欧氏距离超过平均景深的12%
- SVO在建图线程中将图像划分为固定大小的单元格(30×30像素),来确保特征(每个单元格中Shi-Tomasi得分最高的Fast关键点)的均匀分布
- 在图像金字塔的每一层均提取Fast角点来需要与尺度无关的最佳角点
7 Experimental Results
- 实验在MAV搭载的下视相机记录的数据集和手持相机采集的视频序列中进行
- SVO最多使用2个CPU核心
- 将SVO与PTAM的修改版本[2]进行比较
7.1 Accuracy
- 使用文献[31]的方法,将前10帧与真值对齐,来生成误差演变图
- 受到文献[32]的启发,还计算了每秒的平均漂移
- 尺度漂移是通过比较相对平均的欧几里得范数和真值来计算的
- 重投影误差在特征对齐步骤中产生
- local BA的作用并不大
7.2 Runtime Evaluation
- 运动估计线程所需时间分解
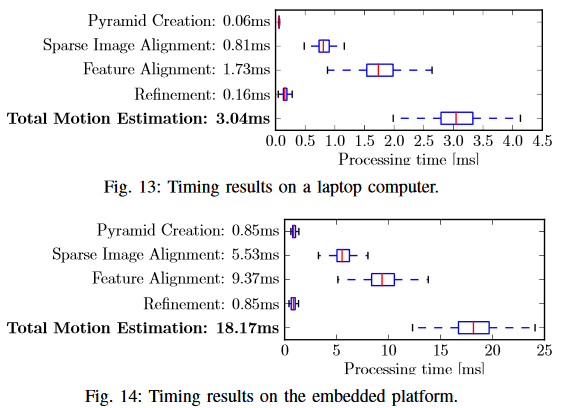
- 建图线程
- 用新帧更新所有深度滤波器所需的时间在很大程度上取决于滤波器的数量
- 选择新的关键帧后滤波器的数量会增多,但随着滤波器收敛会迅速减少
- 平均而言,建图线程比运动估计线程快
7.3 Robustness
- 因为深度滤波器的实验,SVO生成的地图中几乎没有异常点,从而使得SVO即使在重复和高频纹理的场景中(如沥青地面、草地)也能收敛
8 Conclusion
- SVO速度提升的原因是由于运动估计不需要特征提取和匹配